摘要
倒立摆是机器人学中一个非常重要的模型,火箭、导弹、独轮车、双足机器人、四足机器人,基本都是倒立摆的变形。这里是对基本的倒立摆问题的一些研究和思考。
(转自我的CSDN博客)
倒立摆状态反馈控制
问题描述
关于倒立摆的问题描述如下: 如图所示的倒立摆系统。摆的关节连接在一个可移动的小车上,小车由电机驱动,电机水平驱动力为F,摆杆质量为m,小车质量为M,摆长2l。 现在要研究外力F如何能使摆保持垂直的位置。
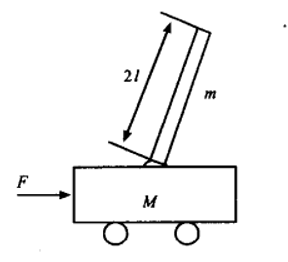
状态空间模型
设摆杆偏离垂直位置角度为θ,小车位移为y。小车对摆水平方向和垂直方向反作用力分别为H和V。
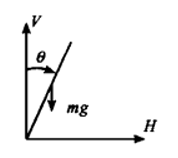 根据牛顿定律可以写出摆水平、垂直方向的力平衡方程:
根据牛顿定律可以写出摆水平、垂直方向的力平衡方程: 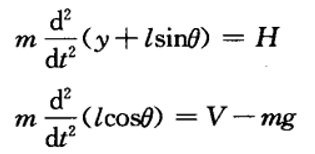 记摆杆对其质心的转动惯量为I,则摆质心的力矩方程为:
记摆杆对其质心的转动惯量为I,则摆质心的力矩方程为: 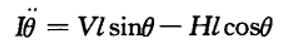 用k表示摩擦系数,小车水平方向的力平衡方程为:
用k表示摩擦系数,小车水平方向的力平衡方程为: 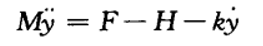 联立以上四个式子,小曲中间变量V、H,得到:
联立以上四个式子,小曲中间变量V、H,得到: 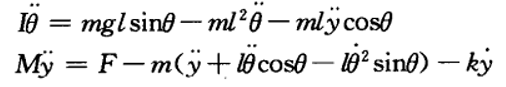 由于θ比较小,这里不妨使sinθ = 0,cosθ = 1,简化方程为:
由于θ比较小,这里不妨使sinθ = 0,cosθ = 1,简化方程为: 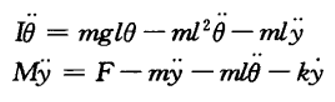 设摆杆质量分布均匀,忽略摩擦(k=0,摩擦力也不会影响能控性),有:
设摆杆质量分布均匀,忽略摩擦(k=0,摩擦力也不会影响能控性),有: 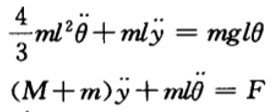 定义系统状态:
定义系统状态: 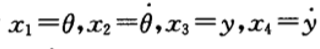 得到状态方程:
得到状态方程:  即:
即:  计算系统的能控性矩阵:
计算系统的能控性矩阵:  能控性矩阵的秩为4,所以系统完全能控。
能控性矩阵的秩为4,所以系统完全能控。
设计状态反馈控制
为了方便设计,不妨设M=2kg,m=0.1kg,l=0.5m。代入状态方程:  其中:
其中: 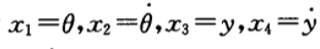 根据极点配置原理,线性定常系统通过状态反馈可以任意配置闭环系统极点的充分必要条件是系统完全能控。 系统的能控性在上面已经证明。 于是采用状态反馈,即:
根据极点配置原理,线性定常系统通过状态反馈可以任意配置闭环系统极点的充分必要条件是系统完全能控。 系统的能控性在上面已经证明。 于是采用状态反馈,即: 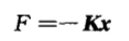 K为4*1矩阵。 原系统的特征多项式为:
K为4*1矩阵。 原系统的特征多项式为: 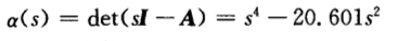 存在大于等于0的极点,显然不加控制的系统是不稳定的,倒立摆不能倒立。 所以我们要配置合适的极点来使得系统达到稳定性要求。
存在大于等于0的极点,显然不加控制的系统是不稳定的,倒立摆不能倒立。 所以我们要配置合适的极点来使得系统达到稳定性要求。
这是一个四阶系统,可以设计两个远离虚轴的极点,和两个靠近虚轴的闭环主导极点,系统的瞬态性能指标主要由主导极点决定。 这样就可以把一个高阶系统简化成一个二阶系统。
典型二阶系统传递函数如下: 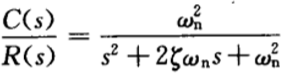
 欠阻尼时的两个特征根为:
欠阻尼时的两个特征根为: 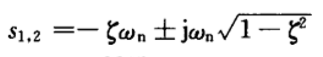 典型二阶系统的瞬态性能指标如下:
典型二阶系统的瞬态性能指标如下:
(1)上升时间: 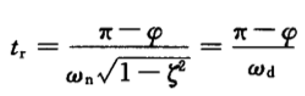 其中
其中 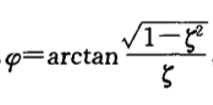 (2)峰值时间:
(2)峰值时间: 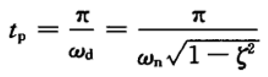 (3)最大超调量:
(3)最大超调量: 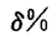
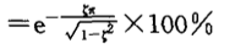 通常取控制系统最大超调量为25% ~ 1.5%,对应的阻尼比为0.4 ~ 0.8 。
通常取控制系统最大超调量为25% ~ 1.5%,对应的阻尼比为0.4 ~ 0.8 。
(4)调节时间:  (5)震荡次数
(5)震荡次数 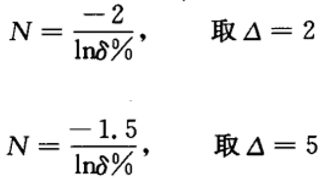 综上,我们想要使系统具有较短的调节时间和适当的超调量,可取
综上,我们想要使系统具有较短的调节时间和适当的超调量,可取 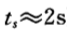
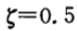 于是闭环主导极点为:
于是闭环主导极点为: 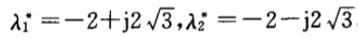 再取两个远离虚轴的极点:
再取两个远离虚轴的极点: 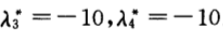 期望特征多项式为:
期望特征多项式为: 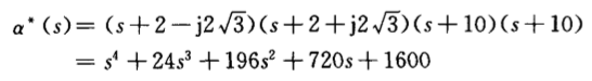 已经有了期望的闭环特征多项式,接下来要如何根据特征多项式确定反馈增益K呢? 有两种常见方法:
已经有了期望的闭环特征多项式,接下来要如何根据特征多项式确定反馈增益K呢? 有两种常见方法: 
 其中算法1在低阶系统中应用会比较方便,但是对于高阶系统,算法2的计算会更为简单。 本问题是四阶系统,我们选用算法2 。 刚刚我们已经计算过原特征多项式。
其中算法1在低阶系统中应用会比较方便,但是对于高阶系统,算法2的计算会更为简单。 本问题是四阶系统,我们选用算法2 。 刚刚我们已经计算过原特征多项式。  我们已经计算出了反馈增益K。
我们已经计算出了反馈增益K。
综上,只需要使得外力输入 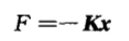 即可使倒立摆保持垂直状态。
即可使倒立摆保持垂直状态。
建立simulink模型
根据A、B、K矩阵画出框图:  给定状态x1(即θ)初值:
给定状态x1(即θ)初值:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ma4KziYv-1590985727990)(C:-user-images-20200525170331331.png)]](https://img-blog.csdnimg.cn/20200601123006150.png)
运行仿真,观测四个状态的变化。
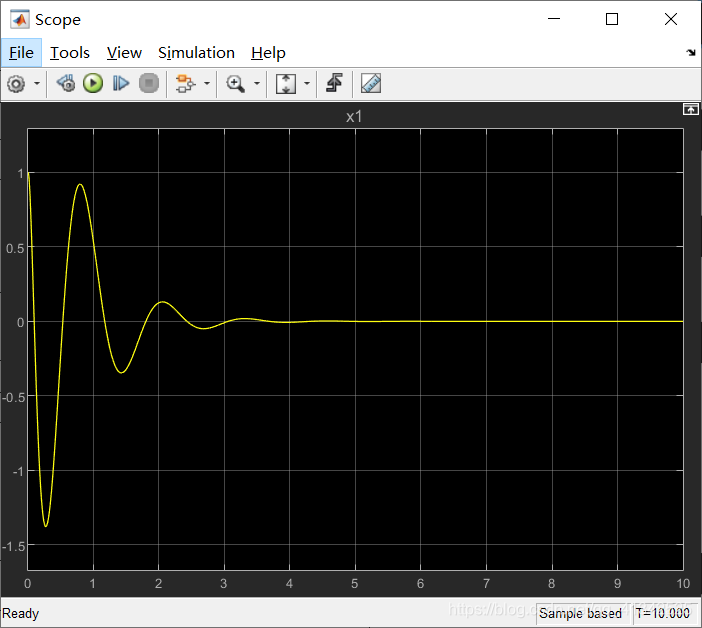
观察x1,可知倒立摆偏离角度在很短时间内收敛到0,控制效果很好。
设计降维状态观测器
在以上的状态反馈控制中,我们使用了4个状态变量来进行反馈控制: 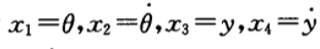 这就意味着,在实际的应用中,我们需要同时用传感器测量4个变量: 摆杆角度、摆杆角速度、小车位移、小车速度。
这就意味着,在实际的应用中,我们需要同时用传感器测量4个变量: 摆杆角度、摆杆角速度、小车位移、小车速度。
但是有的时候,我们不想用这么多传感器,或者有的时候,某些状态量的测量并不方便。 能不能减少反馈的状态个数,同时也能达到控制效果呢?
可以设计降维观测器配合反馈控制来达到目的。
不过在此之前可能有人会想:摆杆角速度和小车的速度不就分别是角度和位移对时间的微分吗? 的确如此,但是直接用微分计算得到的速度与用传感器测得的速度是有不同的。在状态观测器的设计中,用一个状态的微分产生另一个状态的方法通常是不可取的,因为噪声通常比控制信号变化快,信号的微分会使噪声的作用增强,即减小了信噪比。
这里假设摆杆的角度和小车的位移能被测量,即状态
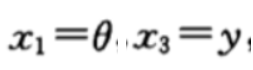
已知,需要设计状态观测器观测其余两个状态。
将状态重新排序: \[ x1 = x,x2=y, x3 = \dot θ,x4= \dot y \] 系统输出为: \[ y=\begin{bmatrix} \theta \\ y\\ \end{bmatrix} \] 状态矩阵变为: \[ A=\begin{bmatrix}0 & 0&1&0 \\ 0 & 0&0&1\\15.244&0&0&0\\-0.363&0&0&0 \end{bmatrix} B=\begin{bmatrix}0 \\ 0 \\-0.741\\0.494 \end{bmatrix} C=\begin{bmatrix}1 & 0&0&0 \\ 0 &1&0&0 \end{bmatrix} \]
降维观测器设计思路:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mhKzq5aO-1590985727998)(C:-user-images-20200531233309196.png)][外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0acABmru-1590985728000)(C:-user-images-20200531233355203.png)][外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cvb2jLCC-1590985728000)(C:-user-images-20200601084105169.png)]](https://img-blog.csdnimg.cn/20200601123049630.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzQyNTI1,size_16,color_FFFFFF,t_70)

 首先判断系统的能观性: \[
Rank Qc = \begin{bmatrix}C \\ CA\\CA^2\\CA^3 \end{bmatrix}=4
\] 系统完全能观,确保可以设计降维状态观测器来观测状态。
首先判断系统的能观性: \[
Rank Qc = \begin{bmatrix}C \\ CA\\CA^2\\CA^3 \end{bmatrix}=4
\] 系统完全能观,确保可以设计降维状态观测器来观测状态。
令 \[ C=\begin{bmatrix}C1 & C2 \end{bmatrix},C1=\begin{bmatrix}1&0\\0&1\end{bmatrix},C2=\begin{bmatrix}0&0\\0&0\end{bmatrix} \] C1非奇异,则状态变换矩阵 \[ P=\begin{bmatrix}1 & 0&0&0 \\ 0 & 1&0&0\\0&0&1&0\\0&0&0&1 \end{bmatrix} \]
\[ \overline A=\begin{bmatrix}0 & 0&1&0 \\ 0 & 0&0&1\\15.244&0&0&0\\-0.363&0&0&0 \end{bmatrix}=\begin{bmatrix}\overline A_{11}&\overline A_{12} \\ \overline A_{21}&\overline A_{22}\end{bmatrix}, \overline B=\begin{bmatrix}0 \\ 0 \\-0.741\\0.494 \end{bmatrix}=\begin{bmatrix}\overline B_{1} \\\overline B_{2}\end{bmatrix}, \overline C=\begin{bmatrix}1 & 0&0&0 \\ 0 &1&0&0 \end{bmatrix} \]
设计反馈增益矩阵:
前面我们在设计状态反馈的时候已经得出了系统的闭环主导极点: \[ \lambda_1^*=-2+j2\sqrt3,\lambda_2^*=-2-j2\sqrt3 \] 一般设计,观测器极点为系统主导极点3~5倍。
我们先试着使极点为-10,-10。
期望特征方程为: \[ \lambda^2+20\lambda+100=0 \] 观测器特征方程为: \[ det(sI-\overline A_{22}+\overline H\overline A_{12})=s^2+(H_{11}+H_{22})s+H_{11}H_{22}-H_{21}H_{22}=0 \]
不妨使: \[ H_{21}=0,H_{22}=0,H_{11}=H_{22} \] 比较系数,得: \[ H_{11}=10,H_{22}=10 \] 子系统的观测器为:
\[ \begin{cases} \dot z=\begin{bmatrix} -10&0 \\0&-10 \end{bmatrix}\hat x_2+\begin{bmatrix} -0.741 \\0.494 \end{bmatrix}u+\begin{bmatrix}15.244&0 \\-0.363&0\end{bmatrix}y\\ \hat x_2=z+\begin{bmatrix} 10&0\\0&10 \end{bmatrix}y \end{cases} \]
原系统的状态观测量为: \[ \hat x=\begin{bmatrix}y\\\hat x_2\end{bmatrix},y=\begin{bmatrix} x_1\\x_2 \end{bmatrix}=\begin{bmatrix} \theta\\y^{'} \end{bmatrix} \] 于是我们便构建了x3、x4,即两个不可测量的速度的观测值。
接下来只需要将观测值代入状态反馈。
建立Simulink模型
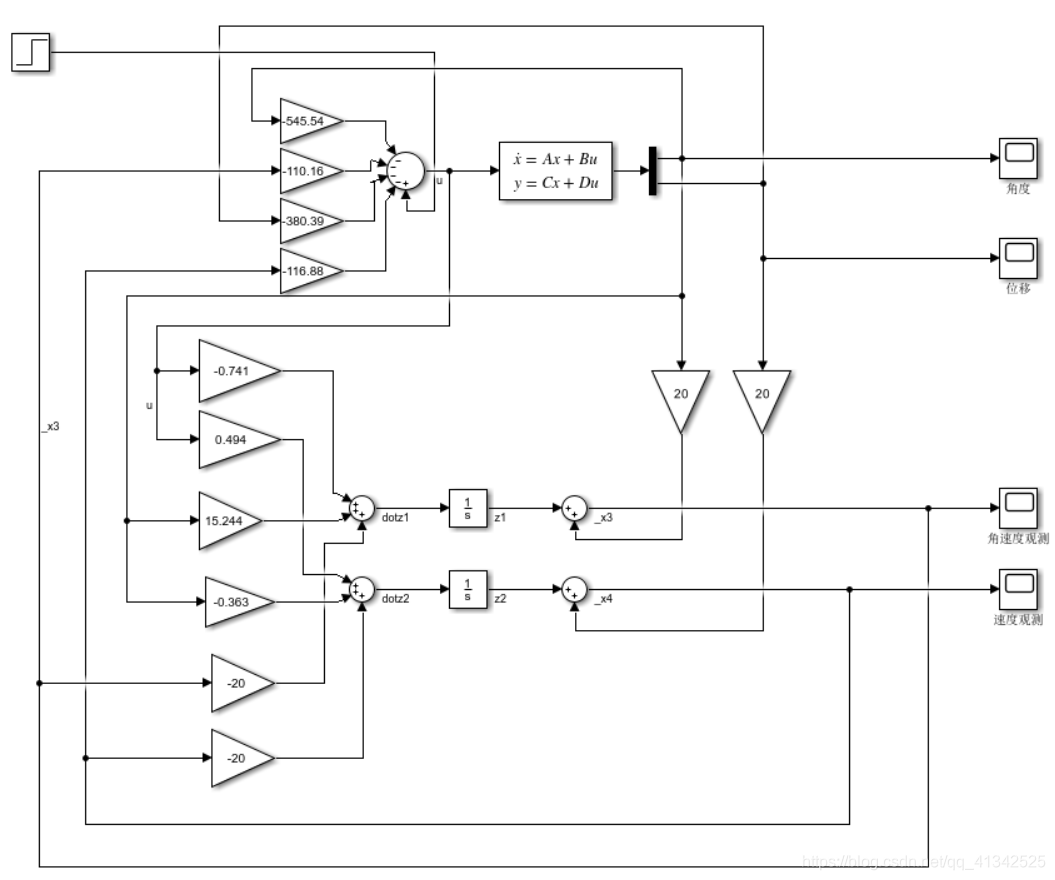
根据以上建立仿真模型:
 为了简化框图,将原系统模型替换成了直接State space表示的形式,具体设置为:
为了简化框图,将原系统模型替换成了直接State space表示的形式,具体设置为:
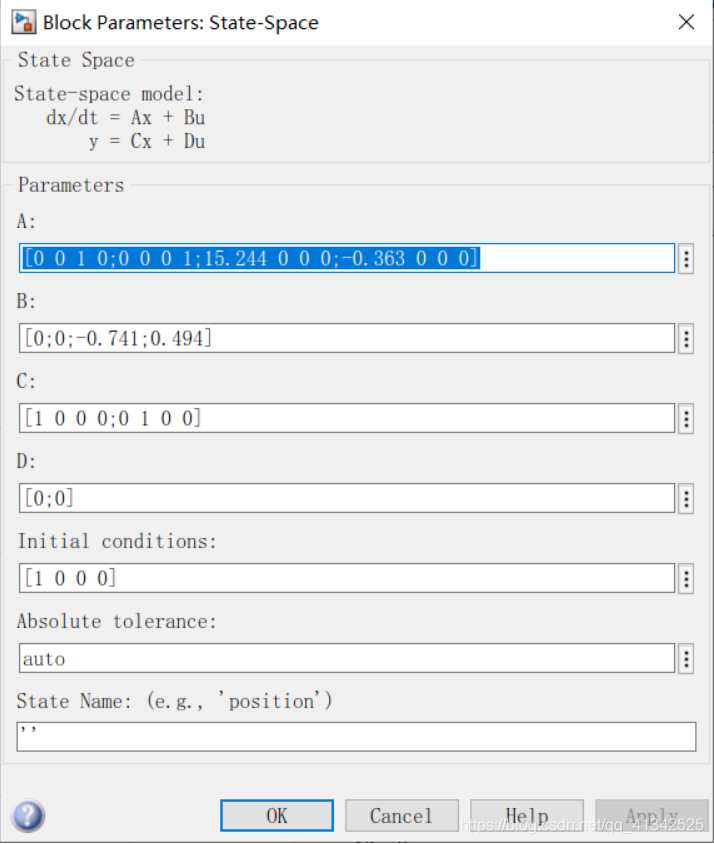
可以看到我们给定了倒立摆角度的初值1,其他全部设为0。
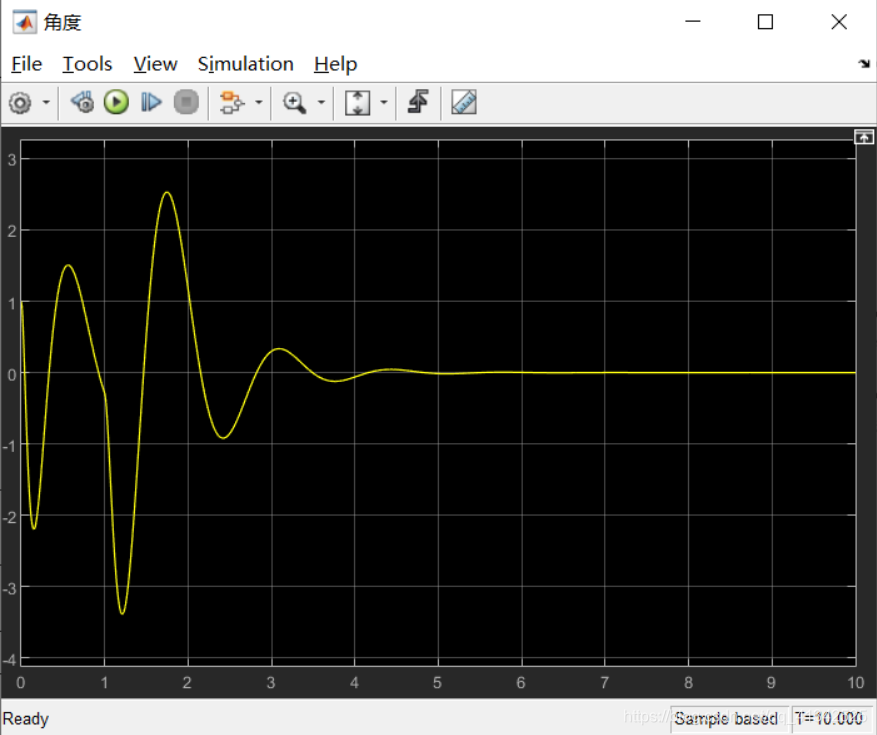
运行仿真,角度scope的输出为:
 系统可以控制倒立摆达到平衡状态,但是超调量和调节时间都增大了。
系统可以控制倒立摆达到平衡状态,但是超调量和调节时间都增大了。
我们试着调整观测器极点,使两极点都为-20:
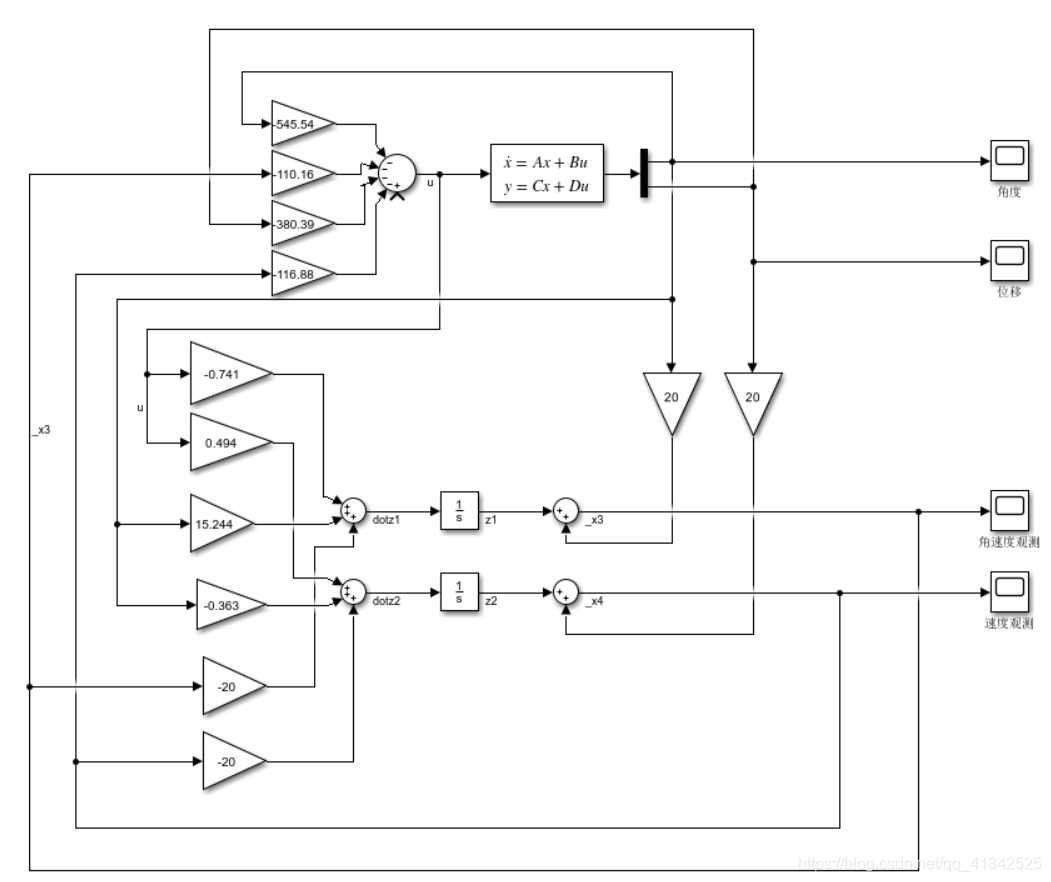
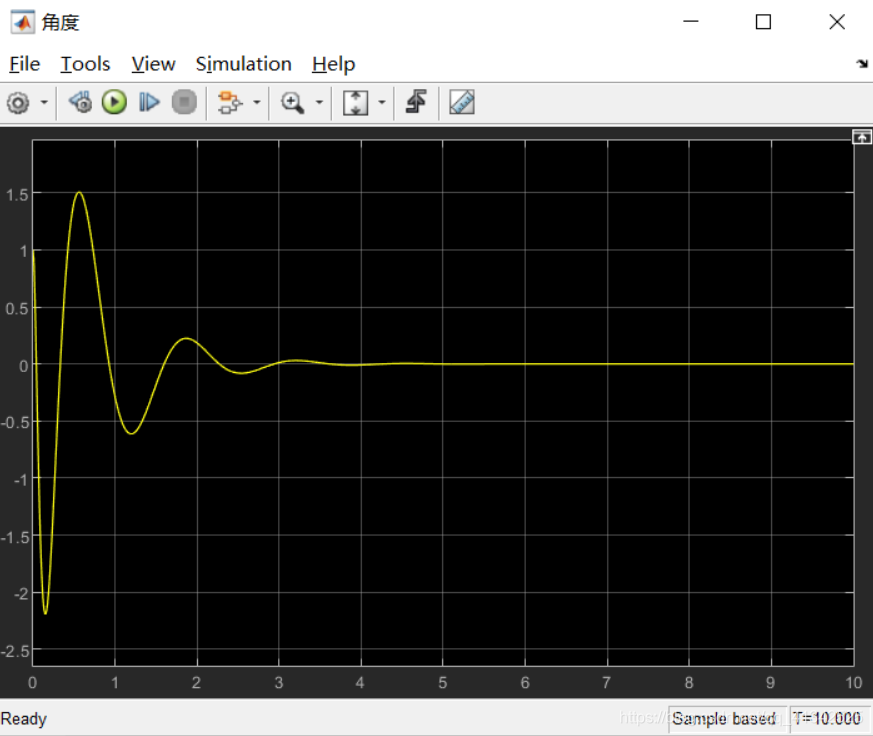
影响并不是很大。
实际上,当我试着将原系统框图完整地画出,并比较观测器观测值与实际状态的误差的时候,发现观测器已经能够很好地跟踪未知状态了。
 θ曲线对比
θ曲线对比
速度曲线对比
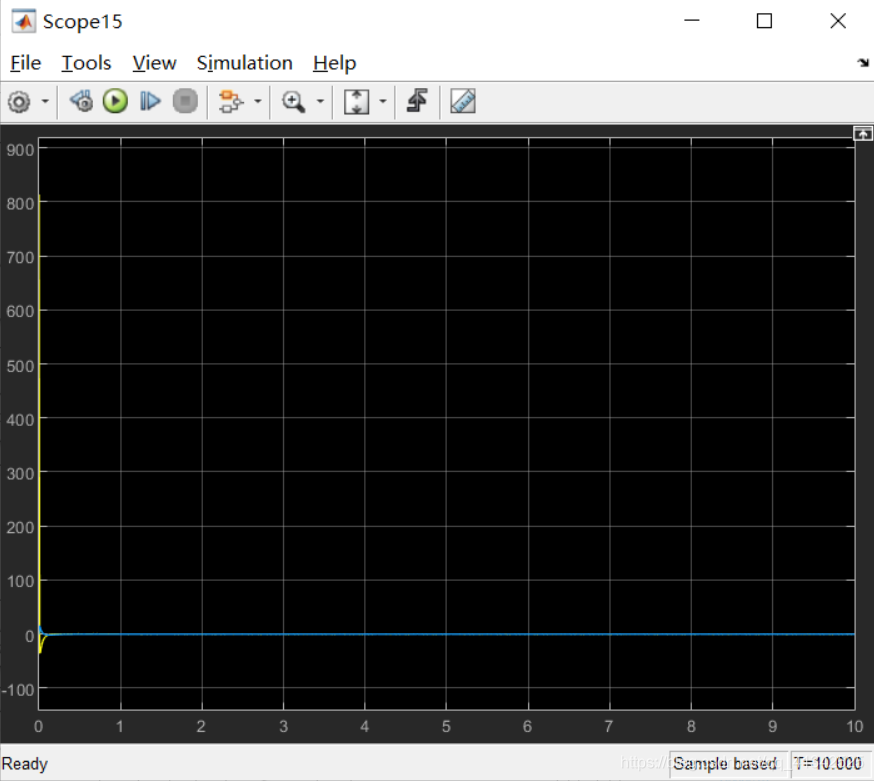
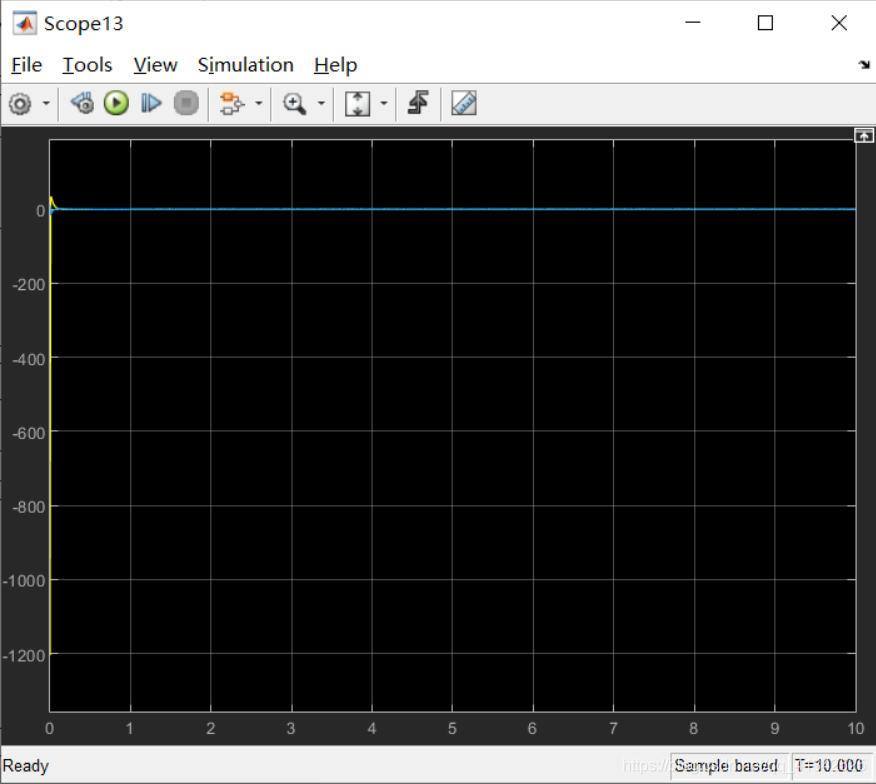
试着在初始状态基础上加入一个阶跃扰动,扰动发生时间为1s,幅度设置较大(1000):
观察到,系统受扰后,仍能迅速调整达到稳定。
总结
综上,倒立摆问题已经基本得到了解决。
只需要通过传感器测量出摆的角度和小车位移,就能设计状态观测器观测出摆的角速度和小车速度,进而通过状态反馈,得到需要输入的外力F。通过此外力F,就能使倒立摆保持平衡。
在实际运用中,根据场景要求,对参数进行优化即可。
matlab模型在我的CSDN个人主页资源中可以找到。